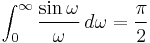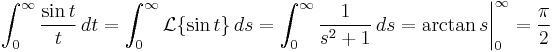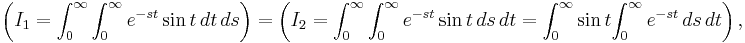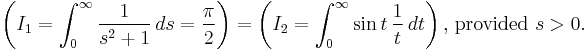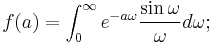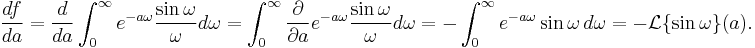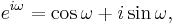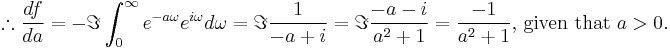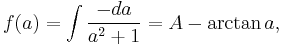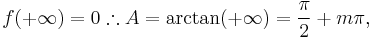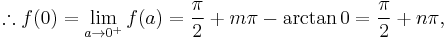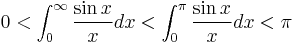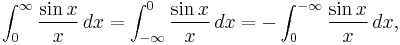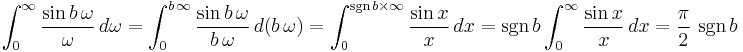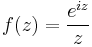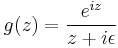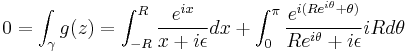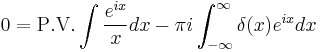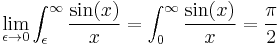Dirichlet integral

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet.

One of those is

\int_0^\infty \frac{\sin \omega}{\omega}\,d\omega = \frac{\pi}{2}

This can be derived from attempts to evaluate a double improper integral two different ways. It can also be derived using differentiation under the integral sign.

Contents

Evaluation

Double Improper Integral Method

Pre-knowledge of properties of Laplace transforms allows us to evaluate this Dirichlet integral succinctly in the following manner:

\int_0^\infty\frac{\sin t}{t}\, dt=\int_{0}^{\infty}\mathcal{L}\{\sin t\}\, ds=\int_{0}^{\infty}\frac{1}{s^{2}%2B1}\, ds=\arctan s\bigg|_{0}^{\infty}=\frac{\pi}{2}

This is equivalent to attempting to evaluate the same double definite integral in two different ways, by reversal of the order of integration, viz.,

\left ( I_1=\int_0^\infty {\int _0^\infty e^{-st} \sin t\, dt}\, ds\right ) = \left ( I_2=\int_0^\infty {\int _0^\infty e^{-st} \sin t\, ds} \, dt = \int_0^\infty \sin t{\int _0^\infty e^{-st}\, ds} \, dt\right ),
\left ( I_1=\int_0^\infty {\frac{1}{s^2%2B1}}\, ds = \frac{\pi}{2}\right ) = \left ( I_2=\int_0^\infty \sin t\, \frac{1}{t} \, dt\right ) \text{, provided } s>0.

Differentiation under the integral sign

First rewrite the integral as a function of variable 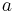\!a. Let

f(a)=\int_0^\infty e^{-a\omega} \frac{\sin \omega}{\omega} d\omega�;

then we need to find 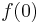\!f(0).

Differentiate with respect to 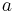\!a and apply the Leibniz Integral Rule to obtain:

\frac{df}{da}=\frac{d}{da}\int_0^\infty e^{-a\omega} \frac{\sin \omega}{\omega} d\omega = \int_0^\infty \frac{\partial}{\partial a}e^{-a\omega}\frac{\sin \omega}{\omega} d\omega = -\int_0^\infty e^{-a\omega} \sin \omega \,d\omega = -\mathcal{L}\{\sin \omega\}(a).

This integral was evaluated without proof, above, based on Laplace trasform tables; we derive it this time. It is made much simpler by recalling Euler's formula,

\! e^{i\omega}=\cos \omega %2B i\sin \omega ,

then,

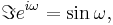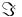\Im e^{i\omega}=\sin \omega, where \Im represents the imaginary part.
\therefore\frac{df}{da}=-\Im\int_0^\infty e^{-a\omega}e^{i\omega}d\omega=\Im\frac{1}{-a%2Bi}=\Im\frac{-a-i}{a^2%2B1}=\frac{-1}{a^2%2B1} \text{, given that } a > 0 .

Integrating with respect to 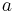\!a:

f(a) = \int \frac{-da}{a^2%2B1} = A - \arctan a,

where 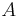\! A is a constant to be determined. As,

f(%2B\infty)=0 \therefore A = \arctan (%2B\infty) = \frac{\pi}{2} %2B m\pi,
\therefore f(0)=\lim _{a \to 0^%2B} f(a) = \frac{\pi}{2} %2B m\pi - \arctan 0 = \frac{\pi}{2} %2B n\pi,

for some integers m & n. It is easy to show that 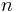\!n has to be zero, by analyzing easily observed bounds for this integral:

0<\int _0^\infty \frac {\sin x}{x}dx < \int _0^\pi \frac {\sin x}{x}dx < \pi

End of proof.

Extending this result further, with the introduction of another variable, first noting that 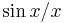\! {\sin x}/{x} is an even function and therefore

\int_0^\infty \frac{\sin x}{x}\,dx = \int_{-\infty}^0 \frac{\sin x}{x}\,dx = -\int_0^{-\infty} \frac{\sin x}{x}\,dx,

then:

\int_0^\infty \frac{\sin b\,\omega}{\omega}\,d\omega = \int_0^{b\,\infty} \frac{\sin b\,\omega}{b\,\omega}\,d(b\,\omega) = \int_0^{\sgn b\times\infty} \frac{\sin x}{x}\,dx = \sgn b \int_0^\infty \frac{\sin x}{x}\,dx = \frac{\pi}{2}\,\sgn b

Complex integration

The same result can be obtained via complex integration. Let's consider

f(z)=\frac{e^{iz}}{z}

As a function of the complex variable z, it has a simple pole at the origin, which prevents the application of Jordan's lemma, whose other hypotheses are satisfied. We shall then define a new function[1] g(z) as follows

g(z)=\frac{e^{iz}}{z %2Bi\epsilon}

The pole has been moved away from the real axis, so g(z) can be integrated along the semicircle of radius R centered at z=0 and closed on the real axis, then the limit 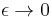\epsilon \rightarrow 0 should be taken.

The complex integral is zero by the residue theorem, as there are no poles inside the integration path

0 = \int_\gamma g(z) = \int_{-R}^R \frac{e^{ix}}{x %2Bi\epsilon} dx %2B \int_{0}^{\pi} \frac{e^{i(Re^{i\theta} %2B \theta)}}{Re^{i\theta} %2Bi\epsilon} iR d\theta

The second term vanishes as R goes to infinity; for arbitrarily small \epsilon , the Sokhatsky–Weierstrass theorem applied to the first one yields

0= \mathrm{P.V.} \int \frac{e^{ix}}{x} dx - \pi i \int_{-\infty}^{\infty}\delta(x) e^{ix} dx

Where P.V. indicates Cauchy Principal Value. By taking the imaginary part on both sides and noting that 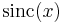\mathrm{sinc}(x) is even and by definition 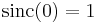\mathrm{sinc}(0)=1 , we get the desired result

\lim_{\epsilon\rightarrow 0}\int_\epsilon^{\infty} \frac{\sin(x)}{x} = \int_0^{\infty} \frac{\sin(x)}{x} = \frac{\pi}{2}

Notes

  1. ^ Appel, Walter. Mathematics for Physics and Physicists. Princeton University Press, 2007, p. 226.

See also

External links